PC
T&P
| |
PERSONAL CONSTRUCT
THEORY & PRACTICE
|
Vol.1 2004 |
| PDF version |
| Author |
| Reference |
| Journal Main |
| Contents 1,1 |
| Impressum |
|
WHEN IS MY GRID COGNITIVELY
COMPLEX AND WHEN IS IT SIMPLE?
SOME APPROACHES TO DECIDING |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Richard C. Bell |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Department of Psychology, University of Melbourne, Australia | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| INTRODUCTION Indices derived from the repertory grid are sometimes used as indicators of a characteristic of a person’s mental functioning. The oldest and most widely known of these is the notion of cognitive complexity-simplicity (Bieri, 1955) which can be assessed in a number of ways in a repertory grid, including some measures based on correlations; the average correlation, the number of factors, or the size of the first eigenvalue. There are a number of others. From a decision-making perspective, such indices require a threshold against which they may be judged. In psychological testing decisions are usually based on the performance of a comparable reference group through norms. Norms however require a standard data format and usage of the repertory grid often occurs in far from standard situations. Another approach is to use statistical significance testing. There have been a few evaluations of indices in grids in this way. Several authors have tested correlations between constructs for a significant difference from zero. For example, Mahklouf-Norris, Jones and Norris (1970) proposed a system termed ‘articulation’ (which can be interpreted in terms of cognitive simplicity – complexity) and identified construct groupings by identifying correlations significantly greater than zero at the .05 level. There are several problems associated with this approach. A number of significance tests are conducted at the same time, the correlations are not independent of each other, and the testing is not simple for the sample sizes (i.e., the numbers of elements) involved. Since the number of elements does not approach the sample size required for normal distribution testing, t-tests involving degrees of freedom are involved. Figure 1 below shows the level of significance for a correlation to be different from zero at the .05 level. 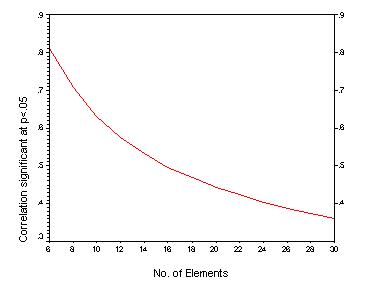 One strategy adopted elsewhere in psychometrics is the evaluation of indices by comparison with distributions of such indices from random data. Horn (1965) proposed using such an approach to the determination of the number of components in factor analysis, and Spence and Ogilvie (1973) and others advocated its use in evaluating the stress index associated with multidimensional scaling. In the grid field Patrick Slater (1977) was first to examine the statistics from grids comprised of random data, with the examination of inter-element distances since such distances are determined by the scale used in making the grid ratings. This work has been extended by Hartmann (1992) and Schoeneich and Klapp (1998) but the principle does not appear to have been extended to a more general consideration of indices in grids. How does this approach compare with the more traditional significance testing above? To examine this, random ratings (on a 1 to 7 scale) were generated for pairs of variables (representing constructs) where the numbers of cases (representing elements) was varied from 6 to 30 in steps of two. For each sample size of elements, 100 replications were carried out. Figure 2 shows the median value of the correlations from random data, and the 95th percentile of the distributions. The significance level from figure 1 is superimposed on this graph for comparison. 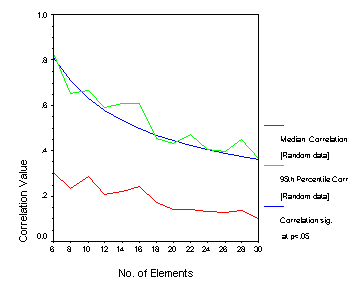 THE DATA Here we considered grids of varying kinds from a number of studies involving different kinds of participants and different kinds of grids. In total there were 834 grids. For each grid 100 replications were constructed by randomly permuting the grid data. The distribution of overall grid ratings thus remained the same, but the structure of the grid in the replications was randomized. 57% of these grids had average correlations (intensity) greater than that of the value associated with 95th percentile of the distribution of correlations from random data. If we look at variance associated with the first factor, then 88% of the 834 grids have first factor variances greater than that associated with the 95th percentile of the distribution of first factor variance of random data. It is well-known that intensity and first factor variance correlate strongly. For these grids the correlation was 0.98. It is somewhat disconcerting therefore that the two indices do not agree with respect to their classification against random data. Table 1 shows the cross-tabulation of classifications. Table 1. Crosstabulation of Av correlation (intensity) permuted data classification by PVAFF permuted data classification
The two agree only in 60% of grids and disagree in the other 40%. Bell (2003) and Fransella, Bell, and Bannister (2004, p.118) showed with hypothetical examples, why intensity as an average correlation may not be a good index of complexity or simplicity, since the mean of heterogeneous correlations can be the same as the mean of homogeneous correlations. These present results add to those concerns. There is a different concern with the first factor variance measure. Nearly 12% of grids do not differ from the first factor variance of random data. These grid structures could be described as having no structure or a fragmented structure. But what of the other 88% of grids with first factor variances greater than that associated with the 95th percentile of the distribution of first factor variance of random data? Are these monolithically structured or do they represent cognitively complex systems of constructs? We cannot tell. One solution is to follow the factor analytic strategy of Horn (1969) mentioned above and test the variance associated with each component in turn against its corresponding random distribution. This method of determining the number of factors (known as ‘parallel analysis’) has become fairly widespread in its use as O’Connor (2002) has provided syntax for carrying this out in standard statistical packages. The number of factors, while an obvious candidate for assessing the cognitive complexity evident in a grid, has rarely been examined as such. Kuusinen and Nystedt (1975) compared it with other traditional measures, such as average correlation and variance explained by the first factor, and found it unrelated. One drawback to their approach was that they determined the number of factors by the ‘eigenvalues-greater-than-one’ rule, a rule notable for its failure to correctly determine the number of factors (Wood, Tartaryn and Gorsuch, 1996; Zwick and Velicer, 1982, 1986). However, Bell (2003) has shown an example of how the number of factors can be a better indicator of construct structure than the traditional indices of average correlation and variance explained by the first factor. If we apply this procedure to these grids we obtain the distribution shown in Table 2. Table 2. No. of Components (Parallel Analysis)
One possibility might be that the parallel test is conservative and tends to choose a lower number of factors (see Turner, 1998). Another possibility is the number of random replications being too few (as shown by the discrepancies between the 95th percentile of random data and the theoretical .05 line in Figure 2). Another test commonly used to determine the number of factors is the "minimum average partial correlation" approach devised by Velicer (1976). This test has the advantage of not requiring random data for its computation[1], and has been shown to be able to identify the correct number of factors in simulation studies (Zwick and Velicer, 1982, 1986). After each component is extracted, its effect (and those extracted before it) is "partialled out" of the correlation matrix of original variables (through computing partial correlations) and the average of the resulting partial correlations is calculated. Velicer reasoned that after more and more factors which accounted for the original correlations were partialled out, the resulting partial correlations would approach zero. However when further components were partialled out, components which reflected unique or "noise" components, rather than "common" factors, the average partial correlation would begin to rise. Velicer’s rule was that the number of factors corresponding to the minimum average partial correlation would be closest to the correct number. Table 3 shows the number of components per grid by this rule. While the number of fragmented grids remains similar, there are fewer monolithically structured grids (less than 40% instead 77%). Table 3. No. of Components (Min Av. Partial Correlation)
Unfortunately the results from this test do not correspond closely to those of the parallel approach as Table 4 following shows. Neither are they independent however; with a chi-square test of association being significant (chi-square = 324, df=15, p <.001), numbers of factors correlating 0.36, and percentage of agreement being about 54%. Table 4. Cross-tabulation of No. of Components (Min Av. Partial Correlation) by No. of Components (Parallel Analysis)
Further comparisons of these approaches require external criterion information as a basis for decision making although clearly both approaches provide a basis for deciding about the simplicity or complexity of construct structure which is sufficiently differentiated to allow differential decisions to be made. SUMMARY AND CONCLUSIONS Making decisions about the complexity or simplicity of construct structure has not featured strongly in grid research. One reason for this has been the lack of criteria for making such decisions. At present norms are not really feasible for grids since they demand a standard form, and while statistical testing is not generally available, comparisons with distributions of indices derived from random data provide a promising alternative. This study showed that intensity was an index that provided little useful differentiation in terms of comparison with random baselines. PVAFF was somewhat more informative in identifying grids with a fragmented structure, but could not distinguish between monolithic and complex structures. Determining the number of components, either by comparisons with random data, or through the use of another statistic, the minimum average partial correlation, provides information that enabled grids to be classified as monolithic, complex, or fragmented in structure. While the minimum average partial correlation approach appeared to provide finer discrimination for these grids, the generality of the random comparison approach suggested that it could be useful in evaluating many other grid indices. [1] This measure is included in the current version of GRIDSTAT ( |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| REFERENCES Bieri, J. (1955) Cognitive complexity-simplicity and predictive behavior. Journal of Abnormal and Social Psychology, 51, 263-286. Fransella, F., Hartmann, A. (1992) Element comparisons in repertory grid technique: Results and consequences of a Horn, J.L. (1965) A rationale and test for the number of factors in factor analysis. Psychometrika, 30, 179-185 Kuusinen, J., and Nystedt, L. (1975) The convergent validity of four indices of cognitive complexity in person perception: A multi-index multimethod and factor analytical approach. Scandinavian Journal of Psychology, 16, 131-136. Mahklouf-Norris, F., Jones, H.G., and Norris, H. (1970) Articulation of the conceptual structure in obsessional neurosis. British Journal of Social and Clinical Psychology, 9, 264-274. O’Connor, B.P. (2000) SPSS and SAS programs for determining the number of components using parallel analysis and Velicer’s MAP test. Behavior Research Methods and Instrumentation, 32, 396-402. Schoeneich, F., & Klapp, B.F., (1998) Standardization of interelement distances in repertory grid technique and its consequences for psychological interpretation of self-identity plots: An empirical study. Journal of Constructivist Psychology, 11, 49-58. Slater, P. (1977) The measurement of intrapersonal space by grid technique. Volume 2. Dimensions of intrapersonal space. Spence, Turner, N.E. (1998) The effect of common variance and structure on random data eigenvalues: Implications for the accuracy of parallel analysis. Educational and Psychological Measurement, 58, 541-568. Velicer, W.F. (1976) Determining the number of components from the matrix of partial correlations. Psychometrika, 41, 321-327 Wood, J.M. Tartaryn, D.J., and Gorsuch, R.L. (1996) Effects of under- and overextraction on principal axis factor analysis with varimax rotation. Psychological Methods, 1, 354-365. Zwick, W.R., and Velicer, W.F. (1982) Factors influencing four rules for determining the number of components to retain. Multivariate Behavioral Research, 17, 253-269. Zwick, W.R., and Velicer, W.F. (1986) A comparison of five rules for determining the number of components to retain. Psychological Bulletin, 99, 432-442. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ABOUT THE
AUTHOR Richard Bell, Ph.D., is an Associate Professor of Psychology at the University of Melbourne, Australia. He is interested in practical problems of measurement in clinical, organizational and educational settings. He has written extensively on the analysis of repertory grid data and has authored widely used software for the analysis of such data. E-mail: rcb@unimelb.edu.au. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| REFERENCE Bell, R. C. (2004). When is my grid cognitively complex and when is it simple? Some approaches to deciding. Personal Construct Theory & Practice, 1, 31-36 (Retrieved from http://www.pcp-net.org/journal/pctp04/bell04.html) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Received: 31 Dec 2003 - Accepted: 12 Jan 2004 - Published: 31 Jan 2004 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Last update 31 January 2004 |