PC
T&P
| |
PERSONAL CONSTRUCT
THEORY & PRACTICE
|
Vol.5 2008 |
| PDF version |
| Author |
| Reference |
| Journal Main |
| Contents Vol 5 |
| Impressum |
| |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Using formal concept analysis to analyse repertory grid data | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Peter Caputi and Desley Hennessy | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Introduction Kelly’s (1955) theory of personal constructs provides a unique way of understanding how individuals make sense of events, people, and situations in the world. Kelly argued that people make sense of the world via a process of comparison and contrast referred to as construing. Constructs, and systems of constructs, are used to discriminate between events, objects, and people, thereby providing meaning to a person’s world. Kelly’s repertory grid technique is a method for capturing aspects of an individual’s construct system. What is a repertory grid? Generally, repertory grids consist of elements (the objects, people, and events in a person’s world) and constructs (bi-polar discriminations used to make sense of the world). When administering a repertory grid, a researcher may provide constructs, or the respondent may generate or elicit a set of constructs using certain elicitation methods. Likewise elements can also be elicited or provided by the researcher. The kinds of elements in a grid and the nature of the constructs provide a context for the respondent to identify the relationship between elements and constructs. Most commonly, the respondent will rate elements for each construct within the construct set, although other strategies for associating elements to constructs are available. Let E represent a set of elements and C a set of constructs. Furthermore, assume that it is possible to quantify the extent to which an element is related to a construct. A repertory grid can be thought of as a table of data that represents the relationship between the members, ei, of an element set E and members, cj, of a construct set C. For example, an element ei can be given a rating rij along a construct cj. The relation rij can also be a ranking relation. This definition provides a formal representation of data collected using the repertory grid technique. Some important issues for repertory grid users emerge from formalising a definition of repertory grid (see Presenting a formal definition of a repertory grid also suggests that the joint representation of elements and constructs is also possible. Fransella, However, ordinal relations among constructs are also of interest. Kelly’s (1955) Organisation Corollary explicitly states that ordinal relationships are a defining feature of construct systems. There are approaches that represent the degree of superordinacy-subordinacy among constructs. For instance, Fransella et al. (2004) identify hierarchical classes analysis (De Boeck & Rosenberg, 1988) as one method that attempts such representations. In this paper we revisit the use of formal concept analysis (Wille, 1982; Ganter & Wille, 1999) as an approach to examining not only the joint representation of elements and constructs, but also ways of representing possible ordinal relations present in the data. Formal Concept Analysis Formal Concept Analysis (FCA: Wille, 1982) is a mathematical technique based on lattice theory. Central to FCA is the notion of a concept. The term concept comes from logic and refers to a category which can be used to classify objects. Within the FCA framework a concept is defined as having two parts: (i) the objects that can be categorised using the concept and (ii) the attributes or properties that are shared by the objects belonging to the concept (Wormuth & Becker, 2004). In addition, certain objects have certain attributes; in other words, objects are related to attributes. Taken together, the set of objects, the set of attributes and the relation defined among the objects and attributes is known as a formal context (Wormuth & Becker, 2004). Let’s consider an example based on one given by Lienhard, Ducasse, and Arevalo (2005). Consider a group of people Table 1: A preference table for beverages for six people
A concept is a set of objects having common attributes. In Table 1 we see that ({Sigmund, George}, {orange juice, wine}) is a concept, so is ({Anna, Fay}, {tea, wine}). Table 2 presents the sets of concepts for the context in Table 1. Table 2: Set of concepts for beverage preference example
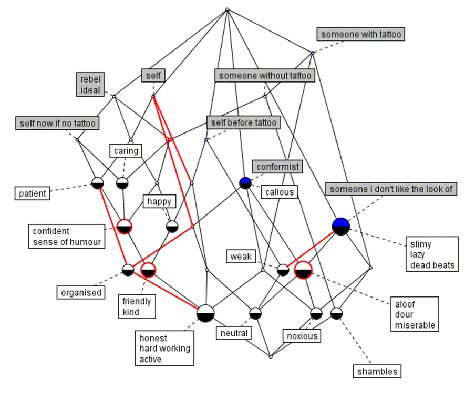
The set of concepts in Table 2 forms a structure known as a complete partial order. A partial order is one way of formally representing or modelling hierarchy in a dataset. Lienhard, Ducasse, and Arevalo (2005, p.75) define a context C as the triple (O, A, R), where O and A are the sets of objects and attributes, and R is a binary relation between O and A. Let X be a subset of O and Y a subset of A, where σ(X) represents all the attributes common to X, and τ(Y) represents all the objects common to Y. A concept is defined as the pair (X,Y) such that Y = σ(X) and X = τ(Y). Further, a concept (X1, Y1) is a subconcept of concept (X2, Y2) if X1 is contained in X2 or equivalently if Y2 is contained in Y1 (Lienhard, Ducasse, & Arevalo, 2005, p.75). Likewise we can define a concept (X1, Y1) as a superconcept of a concept (X2, Y2) if the inverse properties hold (Lienhard, Ducasse, & Arevalo, 2005, p.75). Given these relations, the set of concepts for a context can be represented as a concept lattice. A concept lattice for the concepts in Table 2 is presented in Figure 1. 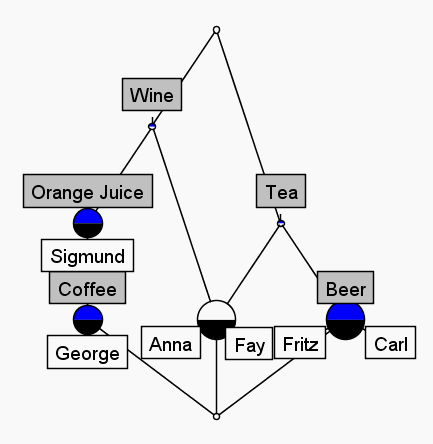 Repertory grids and FCA The basic ideas underpinning FCA have similarities to the formal definition of repertory grids that we presented in Section 2. With FCA, a context is defined by two sets of entities; a set of formal objects, O and a set of formal attributes or properties, A. In addition, we define a relation R that relates members of O to members of A. In this case the relation R is binary, whereas with repertory grids the relation is typically multi-valued (a rating). The similarities, however, are not limited to the model used for generating data. Formal concepts can be ordered, that is, there is a hierarchical order among concepts. Kelly’s (1955) Organisation Corollary posits that constructs are also hierarchically related, that is, there is an ordinal relation among constructs, so that some constructs are subordinate to other constructs, while others are superodinate. Given that formal concepts in FCA can be naturally ordered, the notion of a subconcept-superconcept hierarchy holds. This idea is not dissimilar to the subordinate-superordinate relation that defines the association among constructs. In other words, it is possible to describe the relationships among attributes in terms of implications. Interestingly, the notion of context, namely, the triple of objects, attributes and the relation defined among members of these sets, is an appropriate representation of Kelly’s view that the interpretation of a grid analysis should be made with its context, namely, the set of elements that define the grid. It would appear, then, that on some levels the mathematical framework behind FCA is theoretically consistent with Kelly’s theory. In other words, FCA is a theory-appropriate method of analysing repertory grid data ( There have been applications of FCA to repertory grids. Spangenberg and Wolff (1987) demonstrate how FCA can be applied to a grid elicited from a patient with anorexia. Repertory grids have been applied in the area of knowledge acquisition and numerous studies have adopted FCA as a method of analysing data (see Delugach & Lampkin, 2000; Erdani, Hunger, Werner, & Mertens, 2004; Richards & Compton, 1997). To further illustrate the application of FCA to grid data, we consider the use of repertory grids to explore reasons why people get tattoos. Consider the grid from a 57 year old man with approximately ten tattoos. After obtaining his first tattoo at the age of 19, this man has continued to have tattoos every few years, his most recent being a week before the grid was filled out. Table 3: Grid from man with ten tattoos In order to apply FCA to this grid, we first need to transform multi-valued grid to binary form. In this instance we assign an ‘x’ to a pole if it is rated 1 or 2, and ‘x’ to the contrast pole if it is rated 4 or 5, as per Spangenberg and Wolff (1987). Using this approach, we transform the 12 (construct) x 12 (element) grid to a 24 (poles) x 12 element grid, represented in Table 4. Table 4: Transformed repertory grid (click on heading) We used the program CONEXP -1.3 to analysis this grid (Yevtushenko, 2000) The concept lattice for the grid was extremely complicated, so three self elements (future self, self as I’d like others to see me, and self as others see me) and one pair of construct poles (sociable and hermit-like) were removed to bring out the salient concepts. The resulting concept lattice is given in Figure 2. Figure 2. Concept lattice for context in Table 4. Figure 2 shows that this man sees someone he doesn’t like the look of as slimy, lazy, deadbeats, who are also aloof, dour and miserable. If we take the hierarchies into consideration, he further considers these people to be noxious (his contrast pole to patient) and shambles (his contrast to organised). In addition, it can be seen that he sees a conformist as callous, and himself before he had tattoos as weak and neutral (his contrast pole to caring). However, again the hierarchies here show us he was also happy, friendly, kind, honest, hard working and active. This man’s ideal self is seen as identical to a rebel, with the attributes of happy, friendly, kind, honest, hard working, active, patient, confident, and having a sense of humour. Comparison of FCA and other repertory grid analysis approaches One of the motivations for considering FCA as an alternative approach for analysing grid data is that it allows for a joint representation of elements and constructs. As mentioned in Section 2, there are a number of approaches to spatial representations of elements and constructs. What are the similarities and differences between approaches such as singular value decomposition (SVD), correspondence analysis (CA), multidimensional unfolding (MDU) and FCA? Wolff (1996) conducted a comparison of graphical data analysis methods, including SVD, FCA, MDU, and CA. Table 3 is a summary of some of the features of these spatial representation methods based on Wolff (1996). Table 5: Comparison of FCA and some multivariate methods for analysing repertory grids.
Table 5 distinguishes among the various methods in terms of three features, namely, the analytical model for dealing with the data, the type of joint representation obtained from the analysis, and the primary mechanism underpinning the interpretation of the solution. FCA differs in these three features, but most notably, FCA is able to capture hierarchy, and not just equivalence among entities. Other methods This paper has focused on methods for analysing repertory grids that allows for joint representations of elements and constructs. Methods such as SVD are appropriate and useful methods for determining the extent to which elements and constructs are similar or related to each other. However, such methods do not adequately capture the hierarchical relationship that is assumed among constructs, and the elements associated with those constructs. In this paper we have argued that FCA is a natural model for representing ordinacy in grid data. However, there are other methods that might also be appropriate for capturing the way constructs are organised. As mentioned in Section 2, Fransella et al. (2004) noted the use of hierarchical classes analysis to analyse grids. This technique identifies hierarchies among sets of constructs and elements. While researchers (for example, Gara et al., 1989) have used this technique, Fransella et al. (2004) note that there are some drawbacks to its use given that it is based on Boolean regression and deals only with binary data. Partial order scalogram analysis (POSA: Shye, 1985) is another technique that is worthy of further investigation. POSA is an extension of Guttman’s (1950) unidimensional scaling technique. It is a way of displaying multivariate data in a two-dimensional space. The rows of a data matrix are plotted so that the partial order defined on those rows is maximally preserved. Interestingly, Concluding remark The aim of this paper was to revisit FCA as an alternative approach to analysing repertory grid data. An important advantage of this technique is that it allows hierarchical representations to be captured without loss of information. Future study of the applicability of this technique to repertory grid data is warranted. A version of this paper was presented at the 17th International Personal Construct Psychology Congress, July 16-20, 2007, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| REFERENCES | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De Boeck, P. & Rosenberg, S. (1988). Hierarchical classes: model and data analysis. Psychometrika, 53, 361-381. Delugach, H & Lampkin, B. (2000). Troika: Using grids, lattices and graphs in knowledge acquisition. In G Stumme (ed.) Working with conceptual structures: Contributions to ICCS 200, (pp. 201-214). Aachen, Germany, Shaker Verlag. Erdani, Y., Hunger, A., Werner, S. & Mertens, S. (2004). Ternary grid as a potentially new technique fro knowledge elicitation/acquisition. Second IEEE International Conference on Intelligent Systems. Fransella, F., Ganter, B. & Wille R. (1999). Formal concept analysis: Mathematical foundations. Springer-Verlag. Gara, M.A. Rosenberg, S, Mueller, D.R. (1989). Perception of self and others in schizophrenia. International Journal of Personal Construct Psychology, 2, 253-270. Guttman, L. (1950) The basis of scalogram analysis. In S.A. Stauffer et al (eds). Measurement and prediction Vol4. (pp. 60-90) Kelly, G. A. (1955) The psychology of personal constructs. Vols. I and II. New York: Norton Lienhard, A. Ducasse, S., & Arevalo, G. (2005). Identifying traits with formal concept analysis. ASE ’05, November 7-11, Richards, D., & Shye, S. (1985). Multiple scaling. North-Holland, Spangenberg, N. & Wolff, K. E. (1987). Conceptual grid evaluation. Classification and related methods of data analysis. First conference of the International Federation of Classification Societies, Wille, R. (1982). Restructuring lattice theory: an approach based on hierarchies of concepts. In I. Rival (ed.), Ordered sets. (pp. 445-470). Reidel, Dordrecht-Boston. Wolff, K. E. (1996). Comparison of graphical data analysis methods. In. F Faulbaum & W Bandilla (Eds.), SoftStat '95 Advances in Statistical Software Vol 5 (pp. 139-151), Lucius & Lucius, Wormuth, B. & Becker, P. (2004). Introduction to formal concept analysis. Paper presented at the 2nd International Conference of Formal Concept Analysis, 2004, Sydney Australia. Yevtushenko, S. A. (2000). System of data analysis "Concept Explorer". (In Russian). Proceedings of the 7th national conference on Artificial Intelligence KII-2000, pp. 127-134, Russia, 2000. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ABOUT THE
AUTHORS Peter Caputi, PhD is an Associate Professor in the Peter Caputi, PhD is an Associate Professor in the Email: pcaputi@uow.edu.au  Desley Hennessy is a PhD candidate at the University of Wollongong, Australia. In
addition to her research investigating tattoos as an expression of identity,
she is interested in using her mathematical background in helping students
overcome their hurdles when learning statistics. Desley has a chapter in
Richard Butler’s book on Reflexivity where she examines the application of PCT
to her research as well as herself. Desley Hennessy is a PhD candidate at the University of Wollongong, Australia. In
addition to her research investigating tattoos as an expression of identity,
she is interested in using her mathematical background in helping students
overcome their hurdles when learning statistics. Desley has a chapter in
Richard Butler’s book on Reflexivity where she examines the application of PCT
to her research as well as herself.Email: desley@uow.edu.au |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| REFERENCE Caputi, P. & Hennessy, D. (2008). Using formal concept analysis to analyse repertory grid data. Personal Construct Theory & Practice, 5, 165-173. (Retrieved from http://www.pcp-net.org/journal/pctp08/caputi08.html) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Received: 18 April 2008 – Accepted: 23 October 2008 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
ISSN 1613-5091
| Last update 23 December 2008 |